円の面積の応用問題です。代表的なものから、少しだけひらめきが必要なものまでありますので、色のついた部分の面積を頑張って求めましょう。
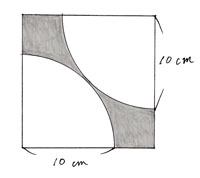 「問題6」 「問題6」
色のついた部分の面積を求めなさい。 |
|
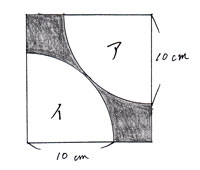
正方形から、白のアとイの部分を引いて求めます。 |
「正方形の面積の求め方」
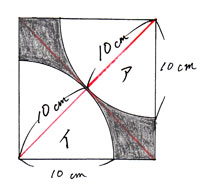
この正方形は1辺の長さがわからないので「ひし形(正方形はひし形と言えます)」と考えて、ひし形の公式に入れて面積を求めます。
アとイは半径10cmのおうぎ形なので、対角線は20cmになります。
ひし形の面積 = 対角線 × 対角線 ÷ 2
よって、この正方形の面積は、20 × 20 ÷ 2 = 200 となります。 |
「アとイの面積の求め方」
アとイは同じ面積で、2つ合わせると半円になるので、
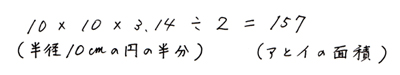
最後に、正方形からアとイの面積を引いて、色のついた部分を求めます。
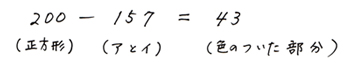
|
|