ある仕事をするのに、A1人では20日、B1人では12日、C1人では15日かかります。
「問題1」
この仕事をはじめから3人ですると、仕事が仕上がるまでに何日かかりますか？ |
仕事全体の量を1とした時、A、B、Cそれぞれの1日あたりにできる仕事量の割合は、
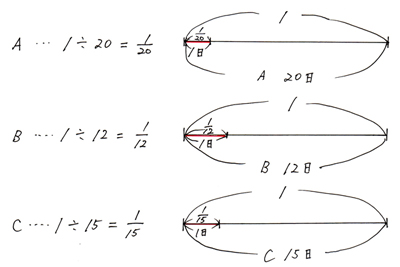
3人でやった1日あたりの仕事量の割合は、3人分の合計だから和を出します。
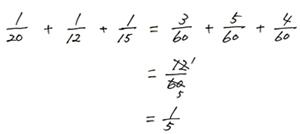
3人で、1日あたり全体の1/5の仕事ができることがわかります。仕事が仕上がるまでに何日かかるかを出すには、全体の1から1/5ずつ「とっていくわり算」で出します。
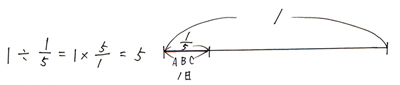
5回とれるので、5日ということです。
「問題2」
この仕事をはじめにBとCの2日で6日間して、その後A1人で仕上げました。仕事が仕上がるまでに全部で何日かかりますか？ |
「問題1」で求めたとおり、
BとC2人でやった1日あたりの仕事量の割合は、2人分の合計だから和を出します。
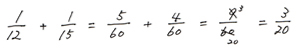
さらに2人で6日間やったのだから、この6倍がBとC2人で6日かけてやった仕事量の割合です。
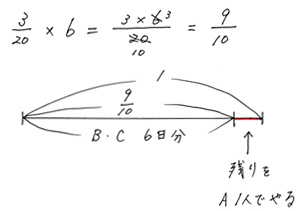
Aが1人でやる量の割合は、全体からBC6日分の割合をひいて出します。
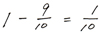
これをA1人でやるのだから、A1人の1日あたりの仕事量でわります。
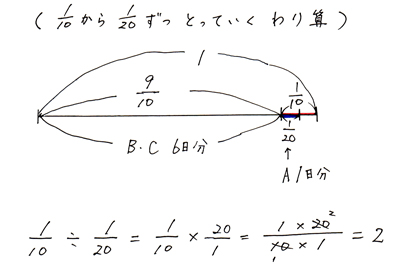
2回とれるので2日分。よってBCで6日、Aだけで2日なので、6+2＝8 となります。
「問題3」
この仕事をはじめから3人でしましたが、途中でCが3日間休みました。仕事が仕上がるまでに全部で何日かかりますか？ |
線分図に表すとこうなります。
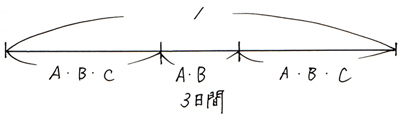
AとBだけで3日間やった仕事量の割合を全体からひけば、ABCの3人でやった仕事量の割合が出せます。
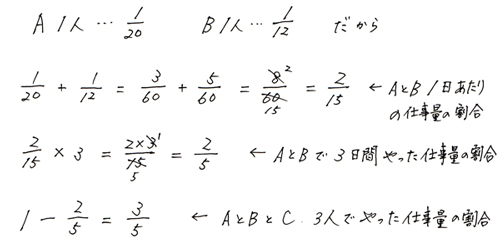
これをABC3人の1日あたりの仕事量の割合でわれば、3人で何日やったかが出せます。ABC3人の1日の仕事量の割合は」問題1」で出したとおり1/5ですから、
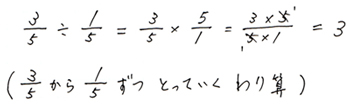
3回とれたので3日です。よってAとBだけで3日間、AとBとCみんなで3日間やったのだから、仕上がるまでにかかった日数は3+3＝6
となります。
|
割合を使って1（応用問題）
割合を使って2（応用問題）
