|
 |
|
| |
算数の基本である「わり算の2つの意味」について解説します。小学生の算数の授業中、毎回のように私の口から出てくる言葉「これはどっちのわり算？」…全てのわり算は「等分のわり算」と「とっていくわり算」に分けることが出来ます。
では、実際に文章題で考えてみましょう。 |
| |
| 「問題1」 |
| 8個のあめがあります。4人の子どもに同じ数ずつあげたとすると、1人分は何個になりますか？ |
| |
まず絵に描いてみましょう。
これを線分図に表すと…
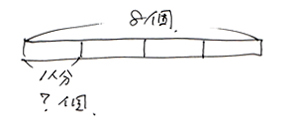
「8個を4等分」して「1人分の数を求める」ことになりますね。
式は 8÷4＝2 となり、答えは「2個」になります。 |
|
|
| |
| では次の問題はどうでしょう？ |
| |
| 「問題2」 |
| 8個のあめがあります。1人の子どもに4個ずつあげるとすると、何人の子どもにあげられるでしょうか？ |
| |
絵に描いてみましょう。
線分図に表すと…
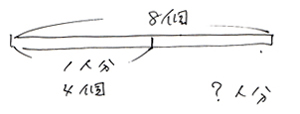
これは数が小さいので、答えは「2人分」と見ただけですぐにわかります。でも、同じ問題でもあめが100個以上あったとしたらすぐにはわかりませんよね。イメージとしてはあめを4個ずつとっていって、1回とれたら1人分、2回とれたら2人分…とし、何回とれるかを考えます。「8個から4個ずつとっていって」「何回とれるかを求める」ことになります。
式は 8÷4＝2 となり、答えは「2個」になります。 |
|
|
| |
これが「とっていくわり算」です。
ただこの呼び方は西村セミナールームだけのもので、本当は正しい名前があります。「等分のわり算」は「等分除」、「とっていくわり算」は「包含除」です…なんだかカッコイイですね。でもやっぱり、塾ではわかりやすく「等分のわり算」と「とっていくわり算」とこれからも言っていきます。
「問題1」も「問題2」も式は同じ「8÷4＝2」なのですが、意味は全然違うのです。
わり算はかけ算の逆で、「問題1」ならば、右の式の
を求めるためのものであり、 |
|
 |
× |
4 |
＝ |
8 |
1人分の数
（1あたりの数） |
|
人数
（いくつ分） |
|
|
|
|
| 「問題2」 ならば、右の式の
を求めるためのものになっています。 |
|
| 4 |
× |
|
＝ |
8 |
1人分の数
（1あたりの数） |
|
人数
（いくつ分） |
|
|
|
|
（1あたりの数）か（いくつ分）か、そのどちらを求めればよい問題なのかということを、文章を読んで理解して式に立てていくことが本当に大切です。
ただ「わり算すれば答えは出るはず」とだけ考えて式を立てていた人は、実はしっかりとわかっていないまま「なんとなく」で解いていたのではないでしょうか？これは先々でつまづく可能性があります。又、お母さん方も「ほら、わればいいじゃない」
と、しっかりとした理由も説明できないままにわり算をさせて、子どもはよくわかっていないまま…ということがありませんか？
この2つのわり算の意味が本当にわかれば、小学校や中学校の文章題はすっきり理解できます。「何倍でしょう？」「単位量あたり」「速さ」などもこれで説明が出来ます。ですから、まずはこの2つの意味を理解して下さい。
理解できたと思ったら、実際に簡単な文章題に挑戦してみましょう！ |
| >> 実践問題に挑戦！ |
| |
| |
 |
| |
「等分のわり算」と「とっていくわり算」
「等分のわり算」と「とっていくわり算」
「等分のわり算」と「とっていくわり算」
