小学校で習う「割合」の最後の応用単元です。しっかりとマスターして中学生になりましょう。まずは基本の問題です。
「問題1」
全体で200ページの問題集があります。全体の3/5は算数の問題で、算数の1/4は計算問題です。計算問題は何ページありますか？ |
順に考えると、まず「全体の3/5は算数の問題」だから、「もと」の「1」にあたるものが「全体」となって、次のような線分図になります。
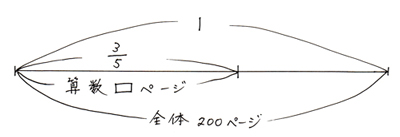
これを言葉の式にすると
これを数字を入れたかけ算式にして、
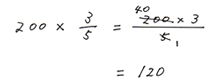
これで算数のページが120ページと出ました。
次に「算数の1/4は計算問題」だから、「もと」の「1」にあたるものが今度は「算数」となって、次のような線分図になります。
これを言葉の式にすると
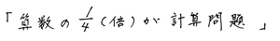
これを数字を入れたかけ算式にして、
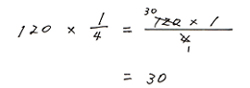
これが計算問題のページ数です。
このように5年生までのやり方で順々に出していっても答えは出せますが、さらにわかりやすくするために、先ほどの2つの線分図を一緒に表してみましょう。
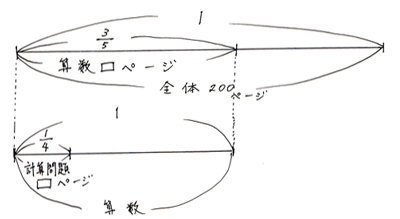
これで全体に対する計算問題のページ数の大きさが1目でわかりますね。これをまとめて言葉の式にすると、
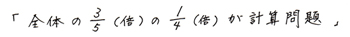
となります。
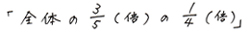
が、はじめの線分図の中でどれだけの割合になるかを出しておきましょう。
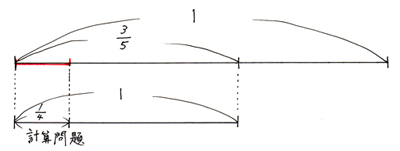
上の線分図の赤線の部分ですね。ここは問題集全体の中の1/4ではありません。
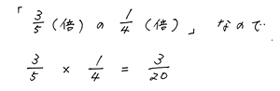
3/20の大きさになりますから、「計算問題」は全体の3/20の割合という事になります。
言葉の式を書き直して、
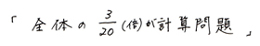
これを数字を入れたかけ算式にして、
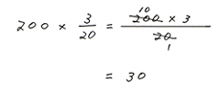
では、次のやり方で、他にも応用問題を解いていきましょう。
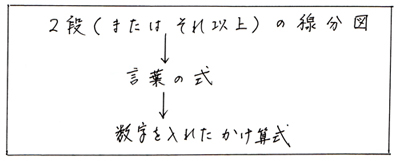
まずは「もと」の数量がわかっていないパターンです。問題1を少し変えてみます。
「問題2」
ある問題集があります。全体の3/5は算数の問題で、算数の1/4は計算問題で30ページあります。この問題集は全体で何ページでしょう？ |
では、2段の線分図にします。
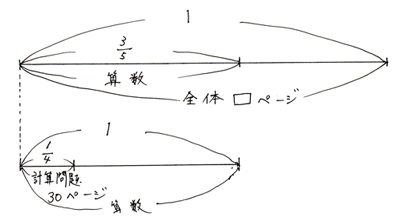
問題1の線分図とほとんど同じですが、違うのは今度は計算問題のページ数が30ページとわかっていて、全体のページ数がわからないというところです。言葉の式は全く同じです。
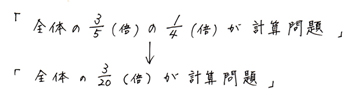
数字を入れた式は、わからないところを 
にして、このままかけ算にします。「全体」のページ数がわかっていないので、ここを
にして、
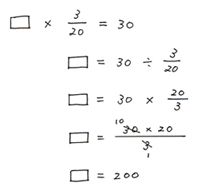
が200とわかったので、 全体が200ページとわかりました。
次は、問題の中に書かれていない割合を自分で出して考えるパターンです。
「問題3」
花子さんは1000円のおこづかいのうち1/4を貯金し、残りの2/3で絵本を買いました。絵本はいくらだったでしょう？ |
線分図にします。この時、絵本は「おこづかいの2/3」でもなく、「貯金の2/3」でもなく、「残りの2/3」なので、残りの割合を自分で計算して出しておきます。「残り」なので、「全体」から「貯金」した割合をひけば出ますね。
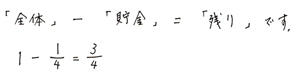
「残り」は全体の3/4という事です。この割合も線分図の中に書き込みます。
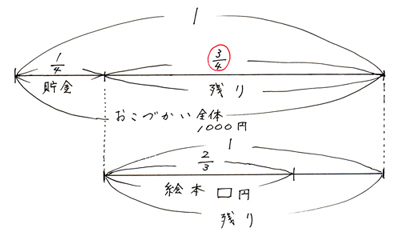
これを言葉の式にして
絵本代の割合がおこづかい全体のどれだけにあたるかを計算で出して、
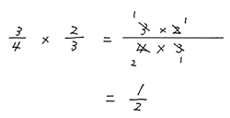
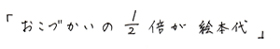
これを数字を入れたかけ算式にして、
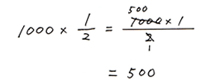
ではこのような要領で、最後に1問挑戦してみましょう。
「問題4」
太郎さんは、家からおばあちゃんの家に行くのに、全体の2/3は電車で行き、その残りの2/3はバスに乗り、最後の2kmは歩きました。家からおばあちゃんの家までは何kmありますか？ |
線分図はこうなります。「残り」と「歩き」の割合を出して、線分図に書き込んで
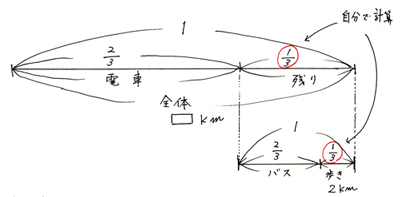
これを言葉の式にすると
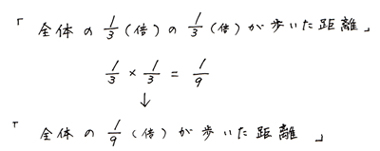
数字を入れたかけ算式は
を使って
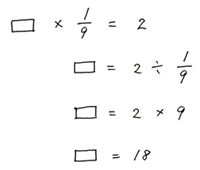
は全体の距離なので、全体の距離が18kmとわかりました。
|
割合を使って2（応用問題）
割合を使って1（応用問題）
