|
 |
|
| |
| それでは、文章題の解答です。考え方の練習ですよ。答えが合っているだけでは意味がありません。線分図もかけましたか？ |
| |
| 「問題1」 |
39人の子どもが長いす1きゃくに5人ずつかけていきました。
1．5人の子どもがかけている長いすは何きゃくありますか？ |
| |
39人の子どもが1脚に5人ずつかけているのだから39人から5人ずつとっていきます。1回とれると1脚、2回とれると2脚…となりますね。
「とっていくわり算」の考え方で、計算は39÷5となり7.8と割り切れますが、7.8脚というのはおかしいですし、5人きっちりかけているいすの数を問われていますので、まさに「5」が何回とれるか「整数」で答えなければいけません。つまり、「商は一の位までしかだしてはいけない、あとは余りとする」と判断します。又、問われている事は5人かけている長いすの数だけですので、答えに余分な事は書きません。式と答えはこちらです。
式は 39÷5＝7 … 4となり、答えは「7脚」になります。
|
| |
| 2．さいごの長いすには、何人の子どもがかけていますか？ |
| |
1の考え方ですと、39人から5人が7回とれて4余っている事になります。この余っている4というのは、もちろん子どもの数です。この4人が最後の長いすに座っている事になりますね。1で書いている式がそのまま利用できますので、改めて式は必要ありません。答えだけでいいですよ。
|
| |
| 3．長いすは全部で何きゃくいりますか？ |
| |
5人かけている長いすが7脚、4人しかかけていない長いすが1脚ですので、もういすの数はわかりますね。
式は 7＋1＝8となり、答えは「8脚」になります。
|
|
|
| |
| 「問題2」 |
| いすが17きゃくあります。1人が2きゃくずつ運びます。全部のいすを運ぶには、何人いればよいですか？ |
| |
17脚から2脚ずつとっていく事になりますね。1回とれたら1人、2回とれたら2人…です。
「とっていくわり算」の考え方で計算は17÷2となり8.5と割り切れますが、1と同様これは人の数ですので、整数で答えなければいけません。よって計算は「商は一の位までしか出してはいけない。あとは余りとする」と判断します。
式は 17÷2＝8…1となります。
2脚を運んでいるのが8人で、余りの1はまだ残っているいす1脚です。これを持っていくのにあと1人必要です。よってもう1つ式を加えて、8＋1＝9となり、答えは「9人」になります。
|
|
|
| |
| 「問題3」 |
| 長さが30cmのテープがあります。このテープから長さ4cmのテープを何本とることができますか？ |
| |
30cmから4cmのテープをとるのですから、まさに「とっていくわり算」の考え方ですね。1回とれると1本、2回とれると2本…となります。
これも「4cmのテープが何本とれるか」と問われているので、整数で答えます。つまり「商は一の位までしか出してはいけない、あとは余りとする」と判断します。又、問われている事以上の余計な事は答えません。式と答えはこちらです。（2cm余っていますが、答えには関係ありません。）
式は 30÷4＝7…2となり、答えは「7本」になります。
|
|
|
| |
| 「問題4」 |
| みかん75個を、1はこに8個ずつ入れて売ります。何はこできますか？ |
| |
75個から8個ずつとって箱に入れていきますね。考え方は「とっていくわり算」で、箱の数を問われているわけですから、今まで同様「商は一の位までしか出してはいけない、あとは余りとする」と判断します。この問題のポイントは、この余りをどう扱うかです。
式は 75÷8＝9…2となります。
この余りの2はみかん2個ですね。もし問題が「みかんを全部入れるには、箱は何箱必要ですか？」ならば、余った2個を入れるための箱がもう1箱必要ですので、答えは10箱となります。でも今回の問題は「みかんを売ります」なので「売りものになる箱が何箱できるか」と聞いているわけです。よって、余ったみかんはそのままにしておきましょう。
答えは「9箱」となります。
|
|
|
| |
| 「問題5」 |
| よしお君の学校の生徒数は1253人です。1人にえんぴつを1本ずつ配るとすると、えんぴつは何ダースあればよいでしょう？1ダースは12本です。 |
| |
まず1253人の生徒に1本ずつ鉛筆を配るためには、鉛筆が1253本必要であると理解しましょう。そのためには何ダースあればよいかという事なので、1ダースは12本ですから1253本から12本ずつとっていく事になります。1回とれたら1ダース、2回とれたら2ダースですね。
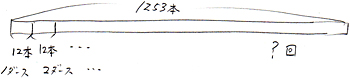
「とっていくわり算」の考え方で、今回も「商は一の位まで、あとは余り」と判断しましょう。
式は 1253÷12＝104…5となります。
さて答えはこの余りをどう考えるかで決まりますね。この余りの5は、鉛筆5本です。1253本から12本が104回とれて5本余っているので、1253本は104ダースと5本という事ですね。この5本のためにあと1ダース用意する必要があります。よって答えはこうなります。
104＋1＝105となり、答えは「105ダース」となります。
|
|
|
| |
| 「問題6」 |
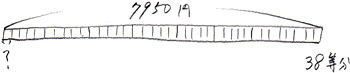
| 38人からお金を同じように集めて、7950円のグローブを買います。少なくとも、1人から何円ずつ集めればよいでしょう？ |
| |
7950円を38人で分けるわけですから、7950を38等分する「等分のわり算」になります。7950円から38円ずつとっていく、「とっていくわり算」ではありません。
計算は7950÷38ですが、お金ですのでこれも商が小数になっては困ります。よって、これも「商は一の位まで、あとは余り」と判断します。
式は 7950÷38＝209 … 8となります。
これは、7950円を38等分すると1人分が209円になって、まだ8円余っているという事です。つまり、38人が209円ずつ出し合ったのでは7980円に8円足りない…という事なのです。だから、7950円のグローブを買うためには、全員があと1円ずつ余分に出す必要があります。7950円より多く集まりますが、仕方ありません。
209＋1＝210となり、答えは「210円」となります。
|
|
|
| |
| 「問題7」 |
| 小麦粉が12.8kgあります。この小麦粉を1.3kgずつ袋につめていくと、小麦粉の入った袋は何袋できますか？又、小麦粉は何kgあまりますか？ |
| |
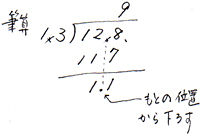 12.8kgから1.3kgずつ袋につめていきますので、12.8から1.3ずつとっていく「とっていくわり算」になります。又、袋の数を問われていますので、これも「商は一の位まで、あとは余りとする」と判断します。気をつける事は、余りの小数点の位置です。
式は 12.8÷1.3＝9…1.1となり、答えは「9袋できて1.1kgあまる」となります。
|
|
|
| |
| 「問題8」 |
| さとうが168.4gあります。ケーキを1個作るのにさとうを15g使うとすると、ケーキは何個作ることができますか？ |
| |
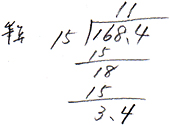 168.4gから15gずつ使ってケーキを作りますので、168.4から15ずつとっていく「とっていくわり算」になります。又、ケーキの個数を問われていますので、「商は一の位まで、あとは余りとする」と判断します。気をつける事は筆算の時、商を一の位できちんと止める事です。
式は 168.4÷15＝11…3.4となり、答えは「11個」となります。
|
|
|
| |
| 「問題9」 |
| お米が45.5kgあります。このお米を毎日同じ量ずつ食べて1週間でちょうどなくなるようにするには、1日何kgずつ食べればよいですか？ |
| |
45.5kgを1週間（7日）で食べきるには、45.5kgを7つに分ける「等分のわり算」になります。
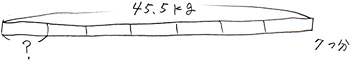
式は 45.5÷7＝6.5となり、答えは「6.5kg」となります。
|
|
|
| |
| 「問題10」 |
| 177人で徒競走の組を作ります。1組の人数ができるだけ同じになるようにして25組作ります。組の人数をどのようにすればよいでしょう？「( ）人の組が（ ）組と、（ ）人の組が（ ）組」…のように答えて下さい。 |
| |
177人を25組に分けるのだから、177を25に分ける「等分のわり算」になります。ただしこれは人なので、「商は一の位まで」としなくてはなりません。すると計算は、177÷25＝7…2となります。これは7人ずつの組が25組できてまだ2人残っている事を意味します。
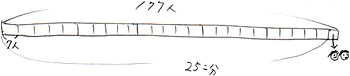
1組の人数をなるべく同じになるようにするのですから、この2人は別々の組に入れてもらえばいいですね。すると8人になる組が2組できる事になります。
式は 177÷25＝7 … 2
25−2＝23となり、答えは「7人の組が23組、8人の組が2組」となります。
|
|
|
| |
| |
 |
| |
「等分のわり算」と「とっていくわり算」
「等分のわり算」と「とっていくわり算」
「等分のわり算」と「とっていくわり算」
