円の面積の応用問題です。代表的なものから、少しだけひらめきが必要なものまでありますので、色のついた部分の面積を頑張って求めましょう。
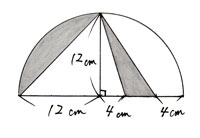 「問題2」 「問題2」
色のついた部分の面積を求めなさい。 |
|
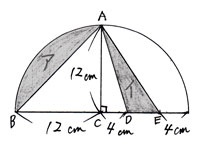
アとイの面積をそれぞれ求めて、足します。 |
「アの部分の求め方」
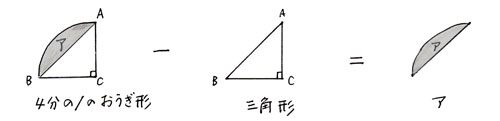
これを式にすると、
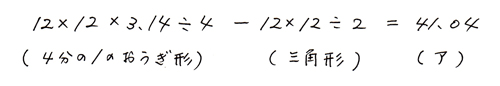
「イの部分の求め方」
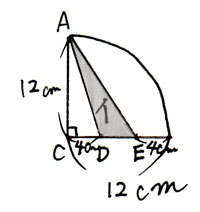
三角形ADE(底辺DE、高さ12cm)の面積として、直接求めます。
底辺DEの長さは、12cmから4cm2つ分を引いて出します。
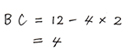
三角形ADEは底辺4cm、高さ12cmだから
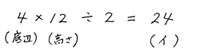
|
アとイを足して、色のついた部分を求めます。
41.04 + 24 = 65.04
|
|