- トップ
- 指導コラム
- わくわく算数学習（工夫して面積を求める -小学生の等積変形-）応用編の解説
|
 |
 わくわく算数学習（工夫して面積を求める -小学生の等積変形-）応用編
|
 |
|
| |
等積変形をして、次の図形の面積を求めてみましょう。
このような形の面積を求める時、2通りのやり方で求める事ができます。
1．三角形ABDの面積と三角形ADCの面積を足す。
2．三角形ABCの面積から、三角形DBCの面積を引く。 |
ところが、この問題はどの三角形も高さがわからないため、1の方法でも2の方法でも求める事ができません。（1の方法で三角形ABDと三角形ADCの高さの合計を12cmとして求める方法はありますが、ここでは省略します。）
そこで、等積変形をして求めてみます。まず、点Bと点Cを通る、ADに平行な2つの直線を引きます。
次にADに対して垂直になるまでBDとCDを上げます。
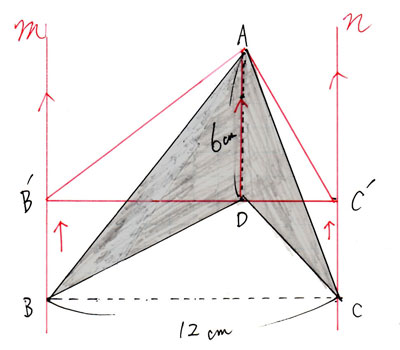
すると、このような形に変わります。
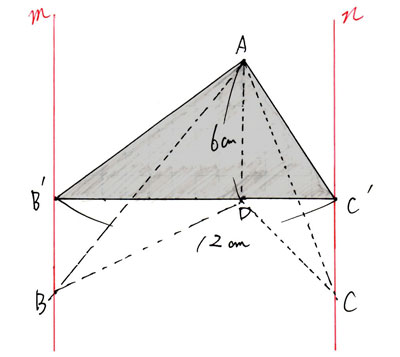
三角形ABDと三角形AB'Dは、どちらも底辺がADで同じ長さです。直線ADと直線mが平行なため、高さも同じです。よって、底辺と高さが等しいため、面積は同じです。三角形ADCと三角形AD'Cも同様に底辺と高さが等しいため、面積は等しくなります。という事は、はじめの図形とこの形を変えた図形の面積は等しいという事になりますね。
この形ならば底辺も高さもわかります。底辺12cmで高さ6cmの三角形です。
（式）
12×6÷2＝36
|
| |
| |
 |
| |
わくわく算数学習（工夫して面積を求める
-小学生の等積変形-）基礎編
