- トップ
- 指導コラム
- わくわく算数学習（工夫して面積を求める -小学生の等積変形-）基礎編の解説
|
 |
 わくわく算数学習（工夫して面積を求める -小学生の等積変形-）基礎編
|
 |
|
| |
この単元は色々な形の面積を工夫によって、さらに形を変えて楽に求めてみようというものです。教科書では長方形を合わせた、次のような形の面積を工夫して求める練習になっています。
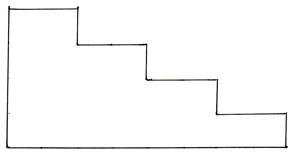
上の図形の面積の求め方は、実際に教科書の中でいろいろな例が紹介されています。
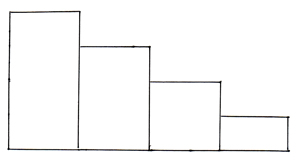
このように縦に切った4つの長方形を…
1段に積み上げて1つの長方形としてみたり、
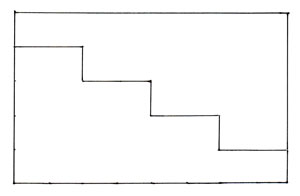
2つを合わせて長方形にして2で割ったり、
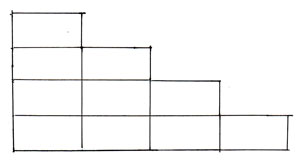
同じ大きさの長方形10個分と考えたりします。このように切ったり組み合わせたりして面積を求めるのです。
では、ワークにある問題をやってみましょう。
「問題」
次のような長方形で、影をつけた部分の面積を求めなさい。その際、下のように形を変形し、2つの三角形の合計として求めなさい。
|
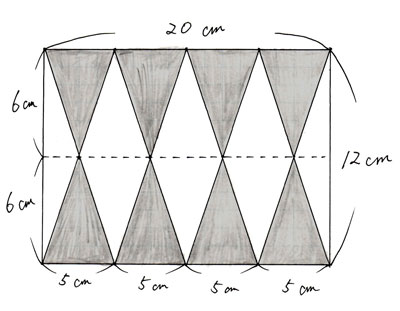
この2つの三角形の面積を求めるのであれば、以下のように各三角形の形を変形させ、
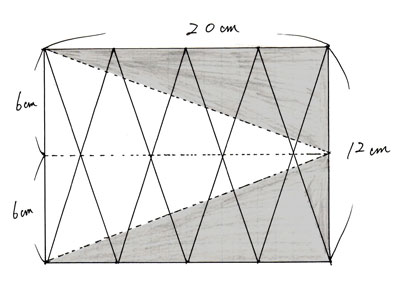
（式）
20×6÷2×2＝120
となりますが、ここでは何故このような形に変形できるのかを考えてみましょう。まずは次の図をご覧下さい。
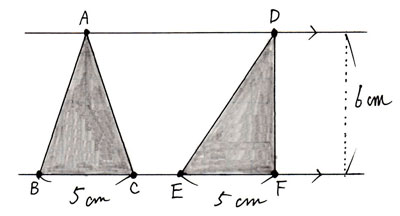
底辺5cm、高さ6cmの三角形ABCとDEFがあります。これら2つの三角形の面積は、5×6÷2＝15c㎡ですね。形は微妙に違いますが、底辺と高ささえ一緒であれば、三角形の面積は等しくなるのです。
では、もっと頂点Aを動かして、Dの位置まで動かしてみましょう。下の図では動かした頂点をA'としています。これでも底辺と高さが同じなので、三角形A'BCと三角形DEFの面積は等しくなります。（見た目がうんと変わっても同じです。）
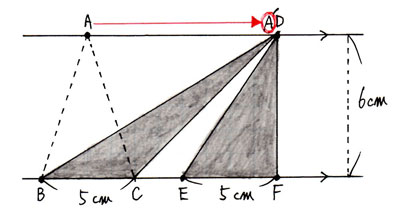
これを、中学生で習う数学用語で「等積変形」と言います。この「等積変形」を使って、ワークの問題を解きます。
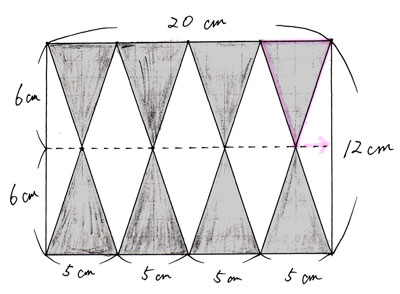
まずは右上の三角形を底辺も高さも変えずに、右端へ寄せて等積変形します。
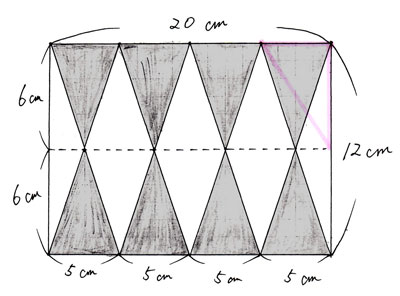
さらにその隣の三角形も右端へ等積変形します。
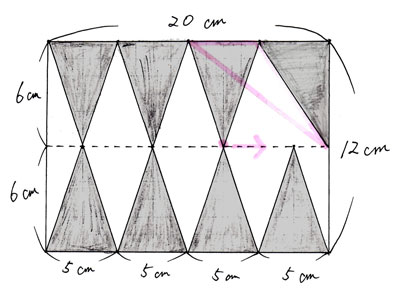
これを全ての影の三角形で行い、等積変形を終えると以下のようになります。
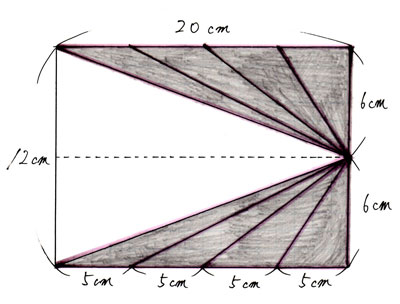
動かしてできたすべての三角形は底辺5cm、高さ6cmなので、動かす前の三角形と面積は変わっていません。よって、合計の面積も同じになります。こうして、「小さい8つの三角形」が「大きい2つの三角形」となったのです。
従って、20×6÷2×2＝120
となるわけですね。 |
| |
| |
 |
| |
わくわく算数学習（工夫して面積を求める
-小学生の等積変形-）応用編
