セミナー通信(vol.229)で説明したとおり、「単位量あたり」は算数の要です。小5からきっちりマスターしていきましょう。では、まず問題です。
「1mの重さが400gの針金があります、この針金2mの重さは何gでしょう?」
簡単ですよね。400×2=800で答えは800gです。ほとんどの人がすぐに答えられたと思います。でも、大切なのはこの式の意味がきちんと説明できる事です。
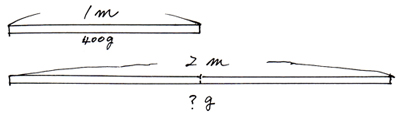
「長さが2倍になったから、重さも2倍になる」…この当たり前の理屈が全ての基本です。長さが何倍になったかがわかれば、重さも何倍になったかがわかります。逆の問題で、重さが何倍になったかがわかれば、長さも何倍になったかがわかります。
「針金の長さと重さ」の関係だけではありません。「水のかさと重さ」も「あめの数と代金」も「ペンキの量とぬる壁の面積」も、これらは全て片方が2倍、3倍…になると、もう片方も同じく2倍、3倍…になるのです。これを「比例の関係」と言います。この事を利用していくと、とてもすっきりとかけ算、わり算の文章題を解く事ができます。
さらに、文章を読んだだけではわかりにくい数量の関係を、自分でわかりやすく整理する方法もあります。それが「単位量図を書く」というやり方です。「単位量図」というのは西村セミナールーム独自の名称なので、この言葉自体は教科書にも載っていなければ参考書や問題集にも載っていません。でも、誰にでも書ける図で、いたってシンプルです。
先ほどの針金問題を単位量図で書くと、このようになります。
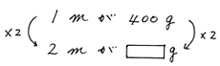
単位量図の書き方にはポイントがあります。
1.4ブロックのうち、左上ブロックに「1(単位)」を書く。(問題に「1」がない時は、小さい方の数を上に書く)
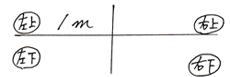
2.残りの数量を各ブロックに入れる。その時…
・縦に同じ単位のものを入れる。(長さどうし、重さどうしなど)
・わからないところを にする。 にする。
3.文章を省略して整理した図なので、真ん中のひらがなもよく考えて書く。(問題によっては「で」になったり「に」になったりします。)
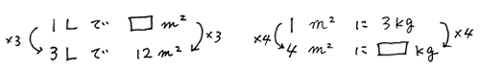
4.上から下への矢印を書きこみ、何倍になっているかをはっきりさせる。 上が「1」の場合はわかりやすいです。例えば…
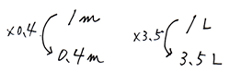
上が「1」でない時は、何倍になっているかを自分で計算して出す。例えば…
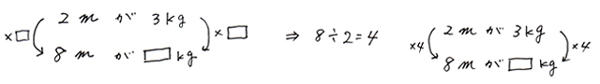
5.左側か右側のどちらかが何倍になっているかわかれば、もう片方にも「かける数」を同じにして書きこむ。左側と右側は必ず「かける数」が同じになります。
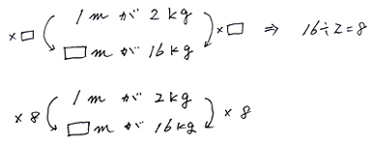
次回は単位量図を実際に完成させる練習です。それまでに単位量図の書き方をしっかりと覚えておいて下さい。 |