約数とは、その数を割り切る事ができる整数の事です。例えば、12を割り切る事のできる整数を「12の約数」と言います。では、どうやって見つけていけばよいでしょうか?…教科書では、1から12までの数を並べて書いてあって、12を割り切る事ができる数に○をつけるようになっていますね。
このやり方ですと20くらいまでの数の約数なら同じように見つけられますが、大きな数…例えば40くらいになってしまうと、1から40まで書いて探すのも大変ですね。100以上の数になってしまうと、約数を全て見つけるのは時間がものすごくかかってしまいます。
さらにこのやり方ですと、約数と気づきにくいものは見落としてしまう可能性があります。例えば54の約数を聞かれて、18や27を見落とさない小5はごくわずかしかいません。1から順に54まで考えて割ってみるだけでも時間がかかって大変なのに、途中のこの数に気づくというのは、数に対してものすごく鋭い小学生以外には至難の業だと思います。
そこで、西村セミナールームのやり方をご紹介します。それは…「約数は2個ずつセットで書き出せ!」です。12の約数を探す時、2で割り切れると分かったら、この2が約数なのはもう決定!さらに12を2で割った答えの6も約数になるという事で、一気に2と6の2つの約数が見つけられるというやり方なんです。
では、具体的にどのようにやっていくか…順にお見せしましょう。12の約数を探す時、1番小さい数から割っていきます。もちろん1です。左端に1を書きましょう。この時に「,(コンマ)」を忘れずに。

12÷1=12で、この答えの12も書きます。今度は右端に。

次に2で割ってみます。割り切れると分かったら、1のとなりに2を書き、12の左どなりに6を書きます。この時も「,(コンマ)」を忘れずに。

次は3を考えてみます。すると割り切れるので、又2のとなりに書き、答えの4も6の左どなりに書きます。もちろん「,(コンマ)」を忘れずに。

順に小さい数から割っていって、3の次の数といえば4ですね。4で割り切れるかと考えようとすると…おっと、4はもう書いてありました。という事で、これで終了です。もう考えなくてもよろしい…つまり、「小さい数(1)から順に割り切れるか考えて、その割った答えを共に書いていき、右にある数にぶつかるまで考えたら終了」なのです。

これで、12の約数全てを書き出す事ができました。3と4の間がずい分あいていますが、気にしなくて構いません。きちんと「,(コンマ)」が書けているかどうかは気にして下さい、( )内の数の配置が「バランスが悪くて気持ち悪い」という人はきれいに書き直して下さいね。
では24の約数を考えてみましょう。
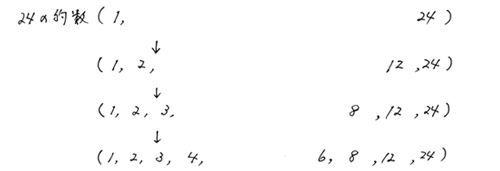
ここまで書いたら4の次の5を考えてみて、割り切れないので書きません。次の6を考えようとしたら…おっと、もう書いてある。という事で「終了〜!」という感じです。
では9の約数を考えてみましょう。

えっ?3が2つ?…そうなんです。9÷3=3で2個セットで書くルールですが、割る数と答えが同じ数になる場合は1つだけ書いて、左からと右からがくっついたら…終了〜!となるわけです。

では、大き目の数…54の約数探しです。
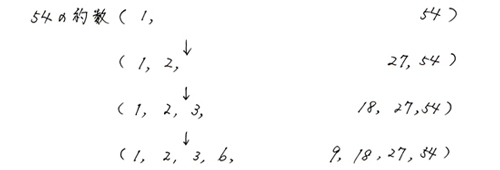
6を考えた後、9までの7、8で割り切れないか考えて終了です。
さらに大きな数…120の約数探しです。
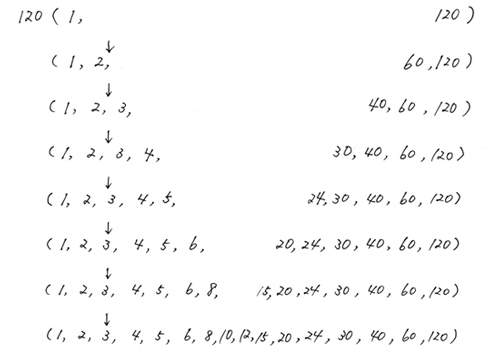
11を考えてみて、割り切れないので終了です。どんなに大きな数でも、このやり方なら見落としがありません。割り算さえ間違えなければ必ず出来ます。
では、やり方はわかったと思いますので、守るべき事を書いておきます。
1.必ず1から始める事。そうすると、同時に「その数(12の約数なら12)」もセットで出てきます。つまり「1」と「その数」は、どんな数の約数にも必ず入っているという事です。
2.÷1から始めたら、順に÷2、÷3、÷4…と1つずつ順に考えて、答えもセットで書いていく事。勝手に思いつくものから書いていってはいけません。見落としの原因となります。
3.1つ書いたら、1つ「,(コンマ)も入れる事。
4.右から来る数とぶつかるところまで、きちんと考えていく事。 |
以上4つを守って、きちんと割り算さえ出来れば、どんな数の約数でも見つけられますよ。「丁寧にきちんと作業できるか」がカギです。 |