|
 |
 直角三角形の合同証明(難) 直角三角形の合同証明(難) |
 |
|
| |
| 直角三角形の合同証明で必ずできるようになってほしい定番問題ですが、難しいので解説します。 |
| |
| 「問題」 |
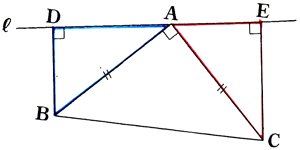
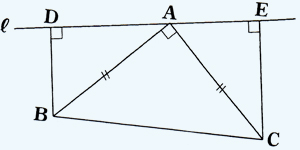 右の図のように、角BAC=90度である直角二等辺三角形ABCがある。Aを通る直線l(エル)にB、Cからそれぞれ垂線BD、CFをひく。この時、三角形ABD=三角形CAEである事を証明せよ。 右の図のように、角BAC=90度である直角二等辺三角形ABCがある。Aを通る直線l(エル)にB、Cからそれぞれ垂線BD、CFをひく。この時、三角形ABD=三角形CAEである事を証明せよ。 |
|
|
| |
直角三角形の合同条件は、通常の三角形の合同条件に加えて
| ・斜辺と1つの鋭角がそれぞれ等しい。 |
| ・斜辺と他の1辺がそれぞれ等しい。 |
この2つが使えるわけですが、今回の場合は「斜辺と1つの鋭角がそれぞれ等しい」が成り立ちますので、ここに導いていきます。まず三角形ABCが直角二等辺三角形ですので、三角形ABD、三角形CAEのそれぞれにおける斜辺は等しくなります。
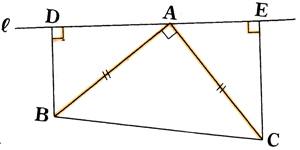 AB=CAです。(対応順に気を付けて) AB=CAです。(対応順に気を付けて)
さらに仮定より角ADBと角CEAが90度という事もわかっています。
角ADB=角CEA=90度 |
では、いよいよ残りは「1つの鋭角が等しい」事の証明です。○と○が等しい理由を以下に示します。
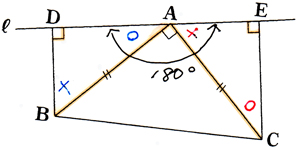 まず○は、直線180度から90度(角BAC)と×(角EAC)をひいた角度です。 まず○は、直線180度から90度(角BAC)と×(角EAC)をひいた角度です。
○=180度−90度−×
○=90度−×
(考え方として○と×の合計が90度になるから、○=90度−×でもいいです。)
一方○は三角形AECの内角の和(180度)から90度(角AEC)と×(角EAC)をひいた角度です。
○=180度−90度−×
○=90度−×
(○の時と同じく、○と×の合計が90度になるから、○=90度−×と考えてもいいです。)
さて、これで○も○も「90度−×」で表されたので、同じ大きさという事がわかりますね。以上より、「斜辺と1つの鋭角がそれぞれ等しい」という事が言えましたので、2つの三角形の合同が証明されます。では以下にきちんと証明します。 |
| |
 三角形ABDと三角形CAEにおいて、 三角形ABDと三角形CAEにおいて、
| 仮定より |
AB=CA
… (1) |
| |
角ADB=角CEA=90度
… (2) |
| また、 |
角BAC |
=90度だから |
| |
角DAB |
=180度-角BAC−角EAC |
| |
|
=90度−角EAC |
| |
|
|
| |
角ECA |
=90度−角EAC |
| よって |
角DAB |
=角ECA
… (3) |
(1)(2)(3)より、直角三角形の斜辺と1つの鋭角がそれぞれ等しいから「三角形ABD=三角形CAE」 |
|
|
| |
| この証明方法は、AとBの大きさが等しい(今回の場合は角DABと角ECA)という事を言うためのもので、「ほら、AもBも同じ言い方で表現されるでしょ。だから同じなんだよ!!」という手法です。今後もいろいろなところで使っていく方法ですので、しっかりマスターしておきましょう。 |
| |
| |
 |
| |